Lab 3: Uniform quantization

Task

The goal of the lab is to learn how to implement uniform quantization and to apply this to signals.

The work should be done in groups of 1 or 2 students.

Examination of the lab is by written report.

Test data

As testdata you will use both pseudo random noise and real world signals.

Memoryless (white) Gaussian noise can be generated by the built-in Matlab function randn.

For memoryless Laplacian noise use this function.

For real world data use this music. Read it to Matlab with audioread.

Uniform quantization

The simplest way to implement uniform quantization is to divide the signal with the stepsize, round to an integer and then multiply with the stepsize again. Since we want to apply some kind of source coding to the quantized data, we will do this in two steps. For example, here is what it would look like for gaussian noise:

x = randn(100000, 1);
delta = 0.03;
q = round(x/delta);

q is now an integer signal, suitable for source coding. If we want to do simple fixed-length coding, we might have to clamp q so it only takes allowed values. For instance, if we are doing fixed-length coding using 8 bits, we can only have 256 different values (in this case from -128 to 127) so we have to clamp like this:

q(q>127) = 127;
q(q<-128) = -128;

However, if we are using some form of source coding, clamping is usually not needed, especially since real world signals have limited amplitude span.

To get the the reconstructed signal we do

xhat = q*delta;

Distortion and SNR

For any type of quantization, the distortion (mean square error) is measured as

D = mean((x-xhat).^2)

and the corresponding SNR as

sigma2 = mean(x.^2)
SNR = 10*log10(sigma2/D)

Simple huffman coding

To perform source coding, do exactly as you did in lab 2: Estimate probabilities for q and then use the huffman function to find the resulting rate.

Rate-SNR performance

Now we can determine how the SNR depends on the rate for our different signals. The rate is controlled by varying the stepsize delta. A large stepsize gives a low rate but also a low SNR. Vice versa, a small stepsize gives a high rate and a high SNR.

Plot rate-SNR curves for all three signals (Gaussian noise, Laplacian noise and music). The curves will look similar to this

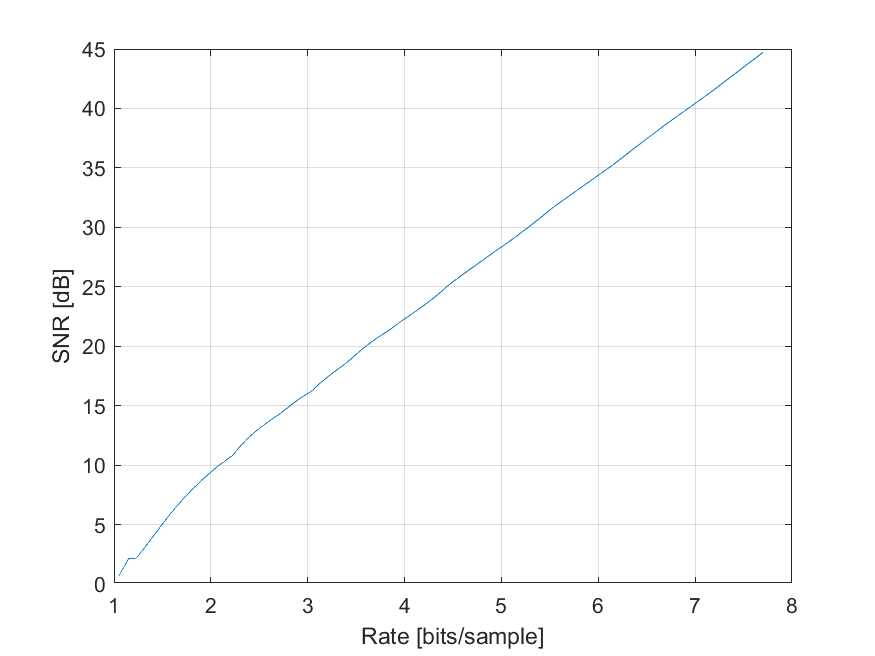
For small stepsizes (ie high rates) the curves are more or less linear, which indicates that the fine quantization approximation holds there.

Suitable choices of stepsizes are such that you get rates between 1 and 8 bits/sample.

Examination

Examination of the lab is by a short written report. Show rate-SNR curves for all three signals. Also include any program code you’ve written.

Send an electronic version of your report (in PDF format) to Harald. Give the name, person number and email adress of every group member.

Deadline

No hard deadline. I would prefer if you send in your reports before the exam period. If you are late, you might have to wait until the next exam period for your points to be reported into Ladok.

Questions?

If you have any questions about the lab, contact Harald.